Optimisation spatiale dans Python : Pulp¶
Pour aller encore plus loin dans la modélisation spatiale, il peut être pertinent de s'intéresser aux méthodes d'aide à la décision. On peut notamment chercher à trouver des solutions optimales à des problématiques spatiales. C'est le domaine de l'optimisation spatiale. Python offre plusieurs possibilités pour travailler dans ce domaine. Ainsi, les bibliothèques PySAL et NetworkX proposent des fonctions permettant de résoudre des problèmes d'optimisation spatiale. Néanmoins, afin d'être plus complet, ce notebook propose d'utiliser la bibliothèque PuLP, spécialement conçu pour résoudre des problèmes d'optimisation linéaire. PuLP s'installe de la manière suivante dans Anaconda :
conda install --channel conda-forge pulp
Si Pulp permet de modéliser et résoudre tous les types de problèmes d'optimisation linéaire, cette bibliothèque requiert de bien connaitre les problèmes en question et leur formalisation mathématique. Il est donc bien d'avoir eu un cours introductif à ces modèles (ou un cours de recherche opérationnelle) pour suivre ce notebook.
Les données utilisées dans ce notebook correspondent à un fichier Excel dans lequel on dispose d'un distancier entre 10 grandes villes françaises.
import pandas as pd
Dist = pd.read_excel("C:/Users/Serge/Desktop/TP_modlocalloc/Pmed_Pref.xlsx", index_col=0, header=0)
Dist
| NICE | LILLE | LYON | NANTES | RENNES | TOULOUSE | BORDEAUX | MARSEILLE | MONTPELLIER | STRASBOURG | |
|---|---|---|---|---|---|---|---|---|---|---|
| NICE | 0.000 | 1055.951 | 409.228 | 1019.384 | 1042.984 | 540.745 | 782.132 | 179.040 | 310.862 | 815.144 |
| LILLE | 1055.951 | 0.000 | 652.594 | 596.315 | 532.329 | 957.003 | 806.610 | 964.910 | 939.084 | 533.105 |
| LYON | 409.228 | 652.594 | 0.000 | 610.814 | 634.414 | 505.319 | 562.635 | 312.974 | 290.427 | 454.860 |
| NANTES | 1019.384 | 596.315 | 610.814 | 0.000 | 193.782 | 573.827 | 328.796 | 911.486 | 780.218 | 821.435 |
| RENNES | 1042.984 | 532.329 | 634.414 | 193.782 | 0.000 | 705.409 | 460.379 | 935.086 | 855.907 | 790.093 |
| TOULOUSE | 540.745 | 957.003 | 505.319 | 573.827 | 705.409 | 0.000 | 248.583 | 392.524 | 231.613 | 956.833 |
| BORDEAUX | 782.132 | 806.610 | 562.635 | 328.796 | 460.379 | 248.583 | 0.000 | 633.911 | 473.001 | 929.115 |
| MARSEILLE | 179.040 | 964.910 | 312.974 | 911.486 | 935.086 | 392.524 | 633.911 | 0.000 | 162.641 | 764.763 |
| MONTPELLIER | 310.862 | 939.084 | 290.427 | 780.218 | 855.907 | 231.613 | 473.001 | 162.641 | 0.000 | 742.217 |
| STRASBOURG | 815.144 | 533.105 | 454.860 | 821.435 | 790.093 | 956.833 | 929.115 | 764.763 | 742.217 | 0.000 |
Le problème de transport¶
Le problème de transport est un problème fondamental en optimisation, particulièrement en recherche opérationnelle. Il modélise une situation courante dans de nombreux domaines, comme celui de la logistique, où il s'agit de déterminer le meilleur moyen de déplacer des biens d'un ensemble d'emplacements (sources) vers un autre ensemble d'emplacements (destinations). C'est un problème d'affectation qui cherche à identifier quelles quantités envoyer d'un lieu (une source) vers un autre lieu (une destination) ?
Ainsi, imaginez que vous avez plusieurs usines produisant un même produit et plusieurs entrepôts où ce produit doit être stocké. Chaque usine possède une certaine quantité de produits à distribuer et chaque entrepôt possède une demande spécifique. Le problème de transport consiste à déterminer combien de produits chaque usine doit envoyer à chaque entrepôt, de telle manière à minimiser le coût total du transport (qui peut dépendre de la distance, du mode de transport, etc.) tout en satisfaisant la demande de chaque entrepôt et en respectant les contraintes de stock.
Plus précisément, ci-dessous nous avons 3 fournisseurs (trois dépôts) disposant de stock de bouteilles d'eau. De l'autre côté, nous avons 4 clients, des points de ventes qui ont une certaine demande en bouteilles d'eau. Nous connaissons les coûts de transport unitaires de ces bouteilles depuis un dépôt i vers un point de ventes j. Le problème de transport consiste à trouver quelles quantités de bouteilles d'eau envoyer depuis un dépôt i vers un point de vente j, de telle sorte à minimiser les coûts de transport induits par ces déplacements. Ce problème peut être représenté sous la forme d'un tableau.
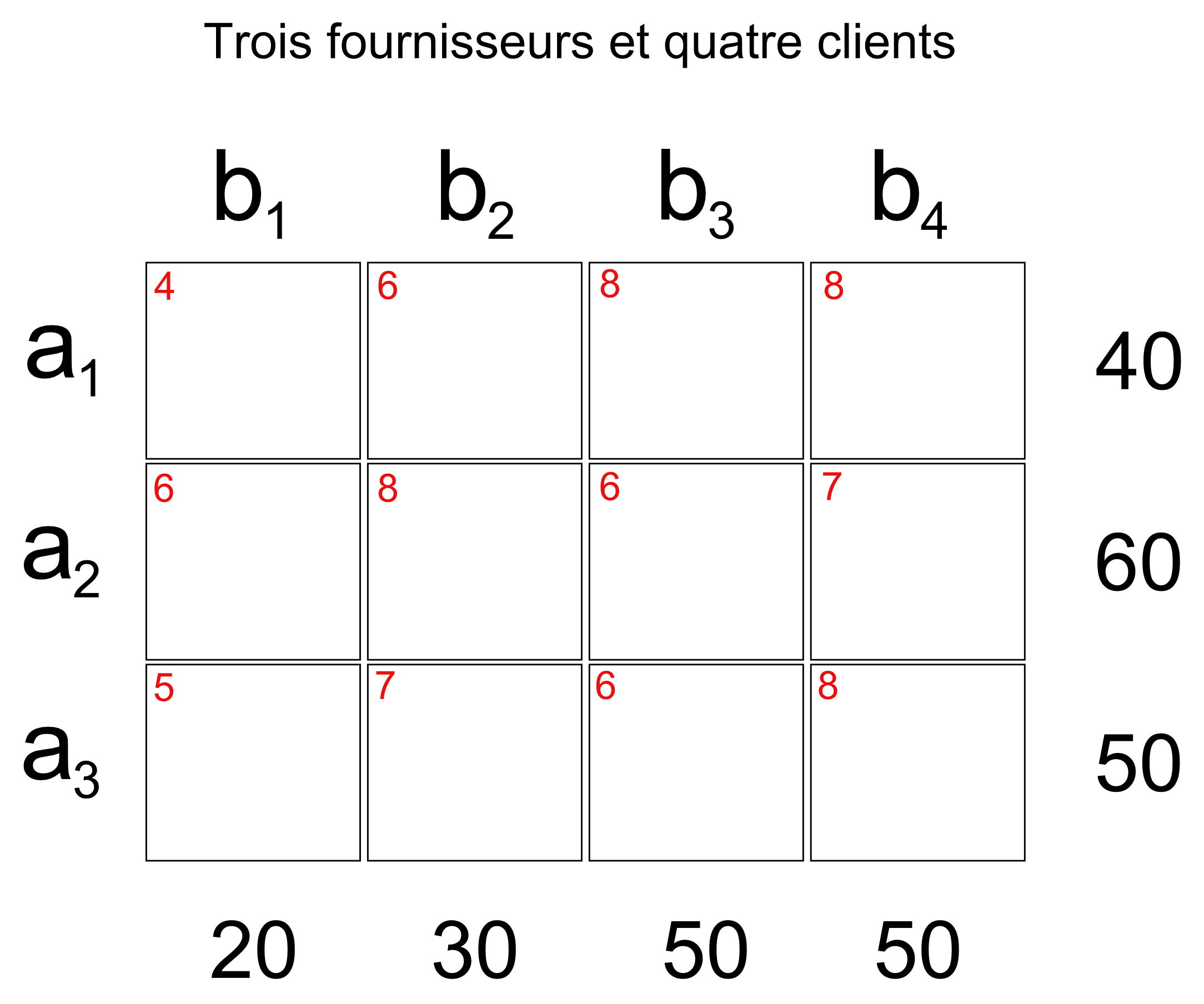
Les valeurs en rouge représentent les couts unitaires de transport, les valeurs à droite représentent les stocks des dépôts i (a1, a2 et a3) et les valeurs en bas représentent les demandes des points de ventes j (b1, b2, b3 et b4). De manière plus générale, le problème de transport peut se formaliser mathématiquement de la manière suivante :
La fonction objectif cherche à minimiser les couts de transport :
Min $\displaystyle \sum_{i=1}^{n} \sum_{j=1}^{m} C_{ij}X_{ij} $
Sous des contraintes de demandes :
$\displaystyle \sum_{i=1}^{n} X_{ij} \ge D_{j}$ $ \forall j$
Sous des contraintes de stocks :
$\displaystyle \sum_{j=1}^{m} X_{ij} \le S_{i}$ $ \forall i$
$C_{ij}$ correspond aux valeurs rouges représentant les couts unitaires de transport. $X_{ij}$ correspond aux quantités qui seront affectées du dépot i vers la destination (le point de vente) j. Il va de soi que $X_{ij} \ge$ 0. On pourra imposer que les $X_{ij}$ soient des entiers. $D_{j}$ correspond à la demande de la destination (le point de vente) j. $S_{i}$ correspond au stock du dépot i.
Si l'on reprend l'exemple présenté ci-dessus, on peut créer les objets suivant pour constituer notre jeu de données dans Python. Pulp nous servira alors à formaliser le problème de manière mathématique sous Python, puis nous servira pour résoudre ce problème.
Depot = ['A1','A2','A3']
Stock = {'A1': 40,
'A2': 60,
'A3': 50}
PtVente = ['B1', 'B2', 'B3', 'B4']
Demande = {'B1': 20,
'B2': 30,
'B3': 50,
'B4': 50}
costs = {'A1': {'B1': 4, 'B2': 6, 'B3': 8, 'B4': 8},
'A2': {'B1': 6, 'B2': 8, 'B3': 6, 'B4': 7},
'A3': {'B1': 5, 'B2': 7, 'B3': 6, 'B4': 8}}
La fonction LpProblem() permet de donner un nom à notre problème et surtout de définir le type d'optimisation : minimisation (LpMinimize) ; maximisation (LpMaximize)... L'objet prob créé pourra stocker une fonction objectif et ensuite on y ajoutera des contraintes.
from pulp import *
prob = LpProblem("Transport", LpMinimize)
Pour déclarer les variables $X_{ij}$, on pourra utiliser la fonction LpVariable.dicts(). Le premier arguments 'X' sert de préfixe aux noms des variables, l'argument (Depot,PtVente) permet de s'appuyer sur les noms des depôts et des points de ventes pour les index des variables, l'argument 0 définit une valeur minimale à ces variables, l'argument None précise qu'il n'y a pas de valeur maximale à ces variables. LpInteger précise que ces variables sont entières. Cela permet de définir nos variables d'affectation qui correspondent aux quantités de bouteilles d'eau à envoyer d'une source i (un dépôt i) vers une destination j (un point de vente j).
# Declaration variable
x_vars = LpVariable.dicts('X', (Depot,PtVente), 0, None, LpInteger)
print(x_vars)
{'A1': {'B1': X_A1_B1, 'B2': X_A1_B2, 'B3': X_A1_B3, 'B4': X_A1_B4}, 'A2': {'B1': X_A2_B1, 'B2': X_A2_B2, 'B3': X_A2_B3, 'B4': X_A2_B4}, 'A3': {'B1': X_A3_B1, 'B2': X_A3_B2, 'B3': X_A3_B3, 'B4': X_A3_B4}}
Pour définir la fonction objectif, il faut en théorie effectuer une double somme. Pour cela, on pourra utiliser la fonction lpSum à laquelle on va appliquer une simple boucle parcourant une liste de toutes les combinaisons possibles entre les dépôts et les points des vente. On se servira de l'objet costs pour associer le cout de transport unitaire à la variable correspondante issue de x_vars. On ajoute (+=) cette somme à notre objet prob.
# Liste de tuples contenant toutes les combinaisons, toutes les routes
x = [(i,j) for i in Depot for j in PtVente]
# Fonction Objectif
prob += lpSum([x_vars[i][j]*costs[i][j] for (i,j) in x])
print(lpSum([x_vars[i][j]*costs[i][j] for (i,j) in x]))
4*X_A1_B1 + 6*X_A1_B2 + 8*X_A1_B3 + 8*X_A1_B4 + 6*X_A2_B1 + 8*X_A2_B2 + 6*X_A2_B3 + 7*X_A2_B4 + 5*X_A3_B1 + 7*X_A3_B2 + 6*X_A3_B3 + 8*X_A3_B4
print(prob)
Transport: MINIMIZE 4*X_A1_B1 + 6*X_A1_B2 + 8*X_A1_B3 + 8*X_A1_B4 + 6*X_A2_B1 + 8*X_A2_B2 + 6*X_A2_B3 + 7*X_A2_B4 + 5*X_A3_B1 + 7*X_A3_B2 + 6*X_A3_B3 + 8*X_A3_B4 + 0 VARIABLES 0 <= X_A1_B1 Integer 0 <= X_A1_B2 Integer 0 <= X_A1_B3 Integer 0 <= X_A1_B4 Integer 0 <= X_A2_B1 Integer 0 <= X_A2_B2 Integer 0 <= X_A2_B3 Integer 0 <= X_A2_B4 Integer 0 <= X_A3_B1 Integer 0 <= X_A3_B2 Integer 0 <= X_A3_B3 Integer 0 <= X_A3_B4 Integer
Pour les contraintes de stocks et de demande, on pourra utiliser une boucle qui parcourt les dépôts et une boucle qui parcourt les points de ventes. Ces boucles ajoutent à l'objet prob des contraintes qui sont des combinaisons linéaires que l'on peut écrire toujours à l'aide de la fonction LpSum(). Les contraintes s'écrivent ensuite comme des tests assez classiques. On ajoute ces contraintes à notre objet prob.
print(lpSum([x_vars['A1'][j] for j in PtVente]) <= Stock['A1'] )
X_A1_B1 + X_A1_B2 + X_A1_B3 + X_A1_B4 <= 40
# Deux familles de contraintes
for i in Depot:
prob += lpSum([x_vars[i][j] for j in PtVente]) <= Stock[i]
for j in PtVente:
prob += lpSum([x_vars[i][j] for i in Depot]) >= Demande[j]
print(prob)
Transport: MINIMIZE 4*X_A1_B1 + 6*X_A1_B2 + 8*X_A1_B3 + 8*X_A1_B4 + 6*X_A2_B1 + 8*X_A2_B2 + 6*X_A2_B3 + 7*X_A2_B4 + 5*X_A3_B1 + 7*X_A3_B2 + 6*X_A3_B3 + 8*X_A3_B4 + 0 SUBJECT TO _C1: X_A1_B1 + X_A1_B2 + X_A1_B3 + X_A1_B4 <= 40 _C2: X_A2_B1 + X_A2_B2 + X_A2_B3 + X_A2_B4 <= 60 _C3: X_A3_B1 + X_A3_B2 + X_A3_B3 + X_A3_B4 <= 50 _C4: X_A1_B1 + X_A2_B1 + X_A3_B1 >= 20 _C5: X_A1_B2 + X_A2_B2 + X_A3_B2 >= 30 _C6: X_A1_B3 + X_A2_B3 + X_A3_B3 >= 50 _C7: X_A1_B4 + X_A2_B4 + X_A3_B4 >= 50 VARIABLES 0 <= X_A1_B1 Integer 0 <= X_A1_B2 Integer 0 <= X_A1_B3 Integer 0 <= X_A1_B4 Integer 0 <= X_A2_B1 Integer 0 <= X_A2_B2 Integer 0 <= X_A2_B3 Integer 0 <= X_A2_B4 Integer 0 <= X_A3_B1 Integer 0 <= X_A3_B2 Integer 0 <= X_A3_B3 Integer 0 <= X_A3_B4 Integer
On pourra générer un fichier pulp (.lp) à l'aide de la fonction writeLP() et surtout on pourra résoudre le problème à l'aide de la fonction solve().
prob.writeLP("Transport.lp")
prob.solve()
1
L'attribut objective permet d'afficher le cout de la solution :
print("Total Cost ", value(prob.objective))
Total Cost 920.0
L'attribut varValue permet d'afficher les affectations correspondantes. On connait alors combien de bouteilles d'eau il faut envoyer depuis un dépôt i vers un point de vente j (20 de A1 vers B1, 0 de A2 vers B1...) afin de minimiser les couts de transport de ces bouteilles d'eau.
for v in prob.variables():
print(v.name, "=", v.varValue)
X_A1_B1 = 20.0 X_A1_B2 = 20.0 X_A1_B3 = 0.0 X_A1_B4 = 0.0 X_A2_B1 = 0.0 X_A2_B2 = 0.0 X_A2_B3 = 10.0 X_A2_B4 = 50.0 X_A3_B1 = 0.0 X_A3_B2 = 10.0 X_A3_B3 = 40.0 X_A3_B4 = 0.0
Le problème p-median¶
Le problème p-median est un autre problème classique en optimisation combinatoire, étroitement lié au problème de transport que nous venons d'évoquer. C'est le problème de localisation-allocation le plus connu. Imaginez que vous deviez choisir p emplacements parmi un ensemble n d'emplacements potentiels pour y installer des services/installations (hôpitaux, écoles, centres de distribution, entrepôts, etc.) constituant l'offre, l'objectif du p-median est de minimiser la distance totale entre chaque demande (clients, maisons, usines, villes...) et le service/installation le/la plus proche.
Le problème p-median consiste à trouver un sous-ensemble de p sites parmi n sites potentiels, de telle sorte que la somme des distances entre chaque demande et le site le plus proche de cet ensemble soit minimale. Il se formalise mathématiquement de la manière suivante :
La fonction objectif cherche à minimiser la somme des distances entre les installations (l'offre) et les lieux de demande :
Min $\displaystyle \sum_{i}^{N} \sum_{j}^{N} X_{i,j} \times D_{i,j}$
Sous contrainte que chaque lieu (demandes/clients/personnes) doit être affecté à une installation :
$\displaystyle \sum_{j}^{N} X_{i,j} = 1 $ $\forall i $
Sous contrainte que le nombre d'installations doit être égal à P :
$\displaystyle \sum_{j}^{N} Y_{j} = P$
Sous contrainte que les lieux (demandes/clients/personnes) ne sont affectés qu'à un site s'il est ouvert :
$\displaystyle \sum_{i}^{N} X_{i,j} \le Y_{j} \times N$ $ \forall j $
Les variables $X_{i,j}$ et $Y_{j}$ sont binaires. $X_{i,j}$ = 0 si l'installation j ne dessert pas le lieu de la demande i. $X_{i,j}$ = 1 si l'installation j dessert le lieu de la demande i. $Y_{j}$ = 0 si l'installation est fermée (n'est pas localisée, positionnée) en j. $Y_{j}$ = 1 si l'installation est ouverte en j. $D_{i,j}$ correspond à la distance entre les lieux de la demande i et les localisations potentielles j des installations. P correspond simplement au nombre d'installations que l'on souhaite "ouvrir".
Pour illustrer ce problème, on pourra prendre le distancier de 10 grandes villes françaises (Pmed_Pref.xlsx). On va alors chercher à identifier dans quelles villes ouvrir 3 entrepôts de telle manière à minimiser les distances à parcourir pour desservir ces 10 grandes villes depuis ces entrepôts. Ces 3 villes à identifier pour localiser nos entrepôts sont parmi ces dix grandes villes. Une ville sera desservie par l'entrepôt le plus proche.
Le fichier Excel permet de stocker les distances dans un objet Dist (DataFrame). Les index et les colonnes de cet objet peuvent être simplement récupérés pour créer un objet Entrepot comprenant les villes possibles d'installation et un objet Ville comprenant les villes à desservir. Ici, les colonnes et les index sont identiques, mais cela pourrait être différent.
import pandas as pd
Dist = pd.read_excel('C:/Users/Serge/Desktop/TP_modlocalloc/Pmed_Pref.xlsx', index_col = 0, header=0)
Ville = list(Dist.index)
Entrepot = list(Dist.columns)
Le problème P-median est encore un problème de minimisation. En revanche, les variables sont binaires : égales à 0 ou à 1. De surcroit, il n'y a pas que des variables d'affectation, il y a aussi des variables d'ouverture (y_vars).
prob = LpProblem("PMED",LpMinimize)
x_vars = LpVariable.dicts('X', (Ville, Entrepot), lowBound = 0, upBound = 1, cat=LpInteger) #Affectation
y_vars = LpVariable.dicts('Y', Entrepot, lowBound = 0, upBound = 1, cat=LpInteger) #Entrepot
La fonction objectif est similaire au problème de transport, il s'agit de minimiser des coûts (plus précisément ici des distances) liés à des affectations origines/destinations.
x = [(i,j) for i in Ville for j in Entrepot]
prob += lpSum([x_vars[i][j]*Dist[i][j] for (i,j) in x])
On vérifiera pour chaque ville que la somme des affectations vaut 1. Ainsi chaque ville est bien affectée à un entrepôt.
for i in Ville:
prob += lpSum([x_vars[i][j] for j in Entrepot]) == 1
On vérifie bien que l'on ouvre le nombre d'entrepôts demandé, ici 3 en récupérant la somme des variables d'ouverture Y (y_vars).
prob += lpSum([y_vars[j] for j in Entrepot]) == 3
Enfin, il ne faut affecter (desservir) des villes qu'à des entrepôts ouverts. Pour cela, il existe plusieurs façons d'écrire cette famille de contraintes. Ici, on prend la somme des affectations réalisées pour chaque entrepôt et on la compare au nombre maximum de villes qu'un entrepôt peut desservir (0 si pas ouvert, 10 si ouvert). Cela fait au final de nombreuses contraintes...
n = len(Ville)
for j in Entrepot :
prob += lpSum([x_vars[i][j] for i in Ville]) <= n * y_vars[j]
print(prob)
PMED: MINIMIZE 806.61*X_BORDEAUX_LILLE + 562.635*X_BORDEAUX_LYON + 633.911*X_BORDEAUX_MARSEILLE + 473.001*X_BORDEAUX_MONTPELLIER + 328.796*X_BORDEAUX_NANTES + 782.132*X_BORDEAUX_NICE + 460.379*X_BORDEAUX_RENNES + 929.115*X_BORDEAUX_STRASBOURG + 248.583*X_BORDEAUX_TOULOUSE + 806.61*X_LILLE_BORDEAUX + 652.594*X_LILLE_LYON + 964.91*X_LILLE_MARSEILLE + 939.084*X_LILLE_MONTPELLIER + 596.315*X_LILLE_NANTES + 1055.951*X_LILLE_NICE + 532.329*X_LILLE_RENNES + 533.105*X_LILLE_STRASBOURG + 957.003*X_LILLE_TOULOUSE + 562.635*X_LYON_BORDEAUX + 652.594*X_LYON_LILLE + 312.974*X_LYON_MARSEILLE + 290.427*X_LYON_MONTPELLIER + 610.814*X_LYON_NANTES + 409.228*X_LYON_NICE + 634.414*X_LYON_RENNES + 454.86*X_LYON_STRASBOURG + 505.319*X_LYON_TOULOUSE + 633.911*X_MARSEILLE_BORDEAUX + 964.91*X_MARSEILLE_LILLE + 312.974*X_MARSEILLE_LYON + 162.641*X_MARSEILLE_MONTPELLIER + 911.486*X_MARSEILLE_NANTES + 179.04*X_MARSEILLE_NICE + 935.086*X_MARSEILLE_RENNES + 764.763*X_MARSEILLE_STRASBOURG + 392.524*X_MARSEILLE_TOULOUSE + 473.001*X_MONTPELLIER_BORDEAUX + 939.084*X_MONTPELLIER_LILLE + 290.427*X_MONTPELLIER_LYON + 162.641*X_MONTPELLIER_MARSEILLE + 780.218*X_MONTPELLIER_NANTES + 310.862*X_MONTPELLIER_NICE + 855.907*X_MONTPELLIER_RENNES + 742.217*X_MONTPELLIER_STRASBOURG + 231.613*X_MONTPELLIER_TOULOUSE + 328.796*X_NANTES_BORDEAUX + 596.315*X_NANTES_LILLE + 610.814*X_NANTES_LYON + 911.486*X_NANTES_MARSEILLE + 780.218*X_NANTES_MONTPELLIER + 1019.384*X_NANTES_NICE + 193.782*X_NANTES_RENNES + 821.435*X_NANTES_STRASBOURG + 573.827*X_NANTES_TOULOUSE + 782.132*X_NICE_BORDEAUX + 1055.951*X_NICE_LILLE + 409.228*X_NICE_LYON + 179.04*X_NICE_MARSEILLE + 310.862*X_NICE_MONTPELLIER + 1019.384*X_NICE_NANTES + 1042.984*X_NICE_RENNES + 815.144*X_NICE_STRASBOURG + 540.745*X_NICE_TOULOUSE + 460.379*X_RENNES_BORDEAUX + 532.329*X_RENNES_LILLE + 634.414*X_RENNES_LYON + 935.086*X_RENNES_MARSEILLE + 855.907*X_RENNES_MONTPELLIER + 193.782*X_RENNES_NANTES + 1042.984*X_RENNES_NICE + 790.093*X_RENNES_STRASBOURG + 705.409*X_RENNES_TOULOUSE + 929.115*X_STRASBOURG_BORDEAUX + 533.105*X_STRASBOURG_LILLE + 454.86*X_STRASBOURG_LYON + 764.763*X_STRASBOURG_MARSEILLE + 742.217*X_STRASBOURG_MONTPELLIER + 821.435*X_STRASBOURG_NANTES + 815.144*X_STRASBOURG_NICE + 790.093*X_STRASBOURG_RENNES + 956.833*X_STRASBOURG_TOULOUSE + 248.583*X_TOULOUSE_BORDEAUX + 957.003*X_TOULOUSE_LILLE + 505.319*X_TOULOUSE_LYON + 392.524*X_TOULOUSE_MARSEILLE + 231.613*X_TOULOUSE_MONTPELLIER + 573.827*X_TOULOUSE_NANTES + 540.745*X_TOULOUSE_NICE + 705.409*X_TOULOUSE_RENNES + 956.833*X_TOULOUSE_STRASBOURG + 0.0 SUBJECT TO _C1: X_NICE_BORDEAUX + X_NICE_LILLE + X_NICE_LYON + X_NICE_MARSEILLE + X_NICE_MONTPELLIER + X_NICE_NANTES + X_NICE_NICE + X_NICE_RENNES + X_NICE_STRASBOURG + X_NICE_TOULOUSE = 1 _C2: X_LILLE_BORDEAUX + X_LILLE_LILLE + X_LILLE_LYON + X_LILLE_MARSEILLE + X_LILLE_MONTPELLIER + X_LILLE_NANTES + X_LILLE_NICE + X_LILLE_RENNES + X_LILLE_STRASBOURG + X_LILLE_TOULOUSE = 1 _C3: X_LYON_BORDEAUX + X_LYON_LILLE + X_LYON_LYON + X_LYON_MARSEILLE + X_LYON_MONTPELLIER + X_LYON_NANTES + X_LYON_NICE + X_LYON_RENNES + X_LYON_STRASBOURG + X_LYON_TOULOUSE = 1 _C4: X_NANTES_BORDEAUX + X_NANTES_LILLE + X_NANTES_LYON + X_NANTES_MARSEILLE + X_NANTES_MONTPELLIER + X_NANTES_NANTES + X_NANTES_NICE + X_NANTES_RENNES + X_NANTES_STRASBOURG + X_NANTES_TOULOUSE = 1 _C5: X_RENNES_BORDEAUX + X_RENNES_LILLE + X_RENNES_LYON + X_RENNES_MARSEILLE + X_RENNES_MONTPELLIER + X_RENNES_NANTES + X_RENNES_NICE + X_RENNES_RENNES + X_RENNES_STRASBOURG + X_RENNES_TOULOUSE = 1 _C6: X_TOULOUSE_BORDEAUX + X_TOULOUSE_LILLE + X_TOULOUSE_LYON + X_TOULOUSE_MARSEILLE + X_TOULOUSE_MONTPELLIER + X_TOULOUSE_NANTES + X_TOULOUSE_NICE + X_TOULOUSE_RENNES + X_TOULOUSE_STRASBOURG + X_TOULOUSE_TOULOUSE = 1 _C7: X_BORDEAUX_BORDEAUX + X_BORDEAUX_LILLE + X_BORDEAUX_LYON + X_BORDEAUX_MARSEILLE + X_BORDEAUX_MONTPELLIER + X_BORDEAUX_NANTES + X_BORDEAUX_NICE + X_BORDEAUX_RENNES + X_BORDEAUX_STRASBOURG + X_BORDEAUX_TOULOUSE = 1 _C8: X_MARSEILLE_BORDEAUX + X_MARSEILLE_LILLE + X_MARSEILLE_LYON + X_MARSEILLE_MARSEILLE + X_MARSEILLE_MONTPELLIER + X_MARSEILLE_NANTES + X_MARSEILLE_NICE + X_MARSEILLE_RENNES + X_MARSEILLE_STRASBOURG + X_MARSEILLE_TOULOUSE = 1 _C9: X_MONTPELLIER_BORDEAUX + X_MONTPELLIER_LILLE + X_MONTPELLIER_LYON + X_MONTPELLIER_MARSEILLE + X_MONTPELLIER_MONTPELLIER + X_MONTPELLIER_NANTES + X_MONTPELLIER_NICE + X_MONTPELLIER_RENNES + X_MONTPELLIER_STRASBOURG + X_MONTPELLIER_TOULOUSE = 1 _C10: X_STRASBOURG_BORDEAUX + X_STRASBOURG_LILLE + X_STRASBOURG_LYON + X_STRASBOURG_MARSEILLE + X_STRASBOURG_MONTPELLIER + X_STRASBOURG_NANTES + X_STRASBOURG_NICE + X_STRASBOURG_RENNES + X_STRASBOURG_STRASBOURG + X_STRASBOURG_TOULOUSE = 1 _C11: Y_BORDEAUX + Y_LILLE + Y_LYON + Y_MARSEILLE + Y_MONTPELLIER + Y_NANTES + Y_NICE + Y_RENNES + Y_STRASBOURG + Y_TOULOUSE = 3 _C12: X_BORDEAUX_NICE + X_LILLE_NICE + X_LYON_NICE + X_MARSEILLE_NICE + X_MONTPELLIER_NICE + X_NANTES_NICE + X_NICE_NICE + X_RENNES_NICE + X_STRASBOURG_NICE + X_TOULOUSE_NICE - 10 Y_NICE <= 0 _C13: X_BORDEAUX_LILLE + X_LILLE_LILLE + X_LYON_LILLE + X_MARSEILLE_LILLE + X_MONTPELLIER_LILLE + X_NANTES_LILLE + X_NICE_LILLE + X_RENNES_LILLE + X_STRASBOURG_LILLE + X_TOULOUSE_LILLE - 10 Y_LILLE <= 0 _C14: X_BORDEAUX_LYON + X_LILLE_LYON + X_LYON_LYON + X_MARSEILLE_LYON + X_MONTPELLIER_LYON + X_NANTES_LYON + X_NICE_LYON + X_RENNES_LYON + X_STRASBOURG_LYON + X_TOULOUSE_LYON - 10 Y_LYON <= 0 _C15: X_BORDEAUX_NANTES + X_LILLE_NANTES + X_LYON_NANTES + X_MARSEILLE_NANTES + X_MONTPELLIER_NANTES + X_NANTES_NANTES + X_NICE_NANTES + X_RENNES_NANTES + X_STRASBOURG_NANTES + X_TOULOUSE_NANTES - 10 Y_NANTES <= 0 _C16: X_BORDEAUX_RENNES + X_LILLE_RENNES + X_LYON_RENNES + X_MARSEILLE_RENNES + X_MONTPELLIER_RENNES + X_NANTES_RENNES + X_NICE_RENNES + X_RENNES_RENNES + X_STRASBOURG_RENNES + X_TOULOUSE_RENNES - 10 Y_RENNES <= 0 _C17: X_BORDEAUX_TOULOUSE + X_LILLE_TOULOUSE + X_LYON_TOULOUSE + X_MARSEILLE_TOULOUSE + X_MONTPELLIER_TOULOUSE + X_NANTES_TOULOUSE + X_NICE_TOULOUSE + X_RENNES_TOULOUSE + X_STRASBOURG_TOULOUSE + X_TOULOUSE_TOULOUSE - 10 Y_TOULOUSE <= 0 _C18: X_BORDEAUX_BORDEAUX + X_LILLE_BORDEAUX + X_LYON_BORDEAUX + X_MARSEILLE_BORDEAUX + X_MONTPELLIER_BORDEAUX + X_NANTES_BORDEAUX + X_NICE_BORDEAUX + X_RENNES_BORDEAUX + X_STRASBOURG_BORDEAUX + X_TOULOUSE_BORDEAUX - 10 Y_BORDEAUX <= 0 _C19: X_BORDEAUX_MARSEILLE + X_LILLE_MARSEILLE + X_LYON_MARSEILLE + X_MARSEILLE_MARSEILLE + X_MONTPELLIER_MARSEILLE + X_NANTES_MARSEILLE + X_NICE_MARSEILLE + X_RENNES_MARSEILLE + X_STRASBOURG_MARSEILLE + X_TOULOUSE_MARSEILLE - 10 Y_MARSEILLE <= 0 _C20: X_BORDEAUX_MONTPELLIER + X_LILLE_MONTPELLIER + X_LYON_MONTPELLIER + X_MARSEILLE_MONTPELLIER + X_MONTPELLIER_MONTPELLIER + X_NANTES_MONTPELLIER + X_NICE_MONTPELLIER + X_RENNES_MONTPELLIER + X_STRASBOURG_MONTPELLIER + X_TOULOUSE_MONTPELLIER - 10 Y_MONTPELLIER <= 0 _C21: X_BORDEAUX_STRASBOURG + X_LILLE_STRASBOURG + X_LYON_STRASBOURG + X_MARSEILLE_STRASBOURG + X_MONTPELLIER_STRASBOURG + X_NANTES_STRASBOURG + X_NICE_STRASBOURG + X_RENNES_STRASBOURG + X_STRASBOURG_STRASBOURG + X_TOULOUSE_STRASBOURG - 10 Y_STRASBOURG <= 0 VARIABLES 0 <= X_BORDEAUX_BORDEAUX <= 1 Integer 0 <= X_BORDEAUX_LILLE <= 1 Integer 0 <= X_BORDEAUX_LYON <= 1 Integer 0 <= X_BORDEAUX_MARSEILLE <= 1 Integer 0 <= X_BORDEAUX_MONTPELLIER <= 1 Integer 0 <= X_BORDEAUX_NANTES <= 1 Integer 0 <= X_BORDEAUX_NICE <= 1 Integer 0 <= X_BORDEAUX_RENNES <= 1 Integer 0 <= X_BORDEAUX_STRASBOURG <= 1 Integer 0 <= X_BORDEAUX_TOULOUSE <= 1 Integer 0 <= X_LILLE_BORDEAUX <= 1 Integer 0 <= X_LILLE_LILLE <= 1 Integer 0 <= X_LILLE_LYON <= 1 Integer 0 <= X_LILLE_MARSEILLE <= 1 Integer 0 <= X_LILLE_MONTPELLIER <= 1 Integer 0 <= X_LILLE_NANTES <= 1 Integer 0 <= X_LILLE_NICE <= 1 Integer 0 <= X_LILLE_RENNES <= 1 Integer 0 <= X_LILLE_STRASBOURG <= 1 Integer 0 <= X_LILLE_TOULOUSE <= 1 Integer 0 <= X_LYON_BORDEAUX <= 1 Integer 0 <= X_LYON_LILLE <= 1 Integer 0 <= X_LYON_LYON <= 1 Integer 0 <= X_LYON_MARSEILLE <= 1 Integer 0 <= X_LYON_MONTPELLIER <= 1 Integer 0 <= X_LYON_NANTES <= 1 Integer 0 <= X_LYON_NICE <= 1 Integer 0 <= X_LYON_RENNES <= 1 Integer 0 <= X_LYON_STRASBOURG <= 1 Integer 0 <= X_LYON_TOULOUSE <= 1 Integer 0 <= X_MARSEILLE_BORDEAUX <= 1 Integer 0 <= X_MARSEILLE_LILLE <= 1 Integer 0 <= X_MARSEILLE_LYON <= 1 Integer 0 <= X_MARSEILLE_MARSEILLE <= 1 Integer 0 <= X_MARSEILLE_MONTPELLIER <= 1 Integer 0 <= X_MARSEILLE_NANTES <= 1 Integer 0 <= X_MARSEILLE_NICE <= 1 Integer 0 <= X_MARSEILLE_RENNES <= 1 Integer 0 <= X_MARSEILLE_STRASBOURG <= 1 Integer 0 <= X_MARSEILLE_TOULOUSE <= 1 Integer 0 <= X_MONTPELLIER_BORDEAUX <= 1 Integer 0 <= X_MONTPELLIER_LILLE <= 1 Integer 0 <= X_MONTPELLIER_LYON <= 1 Integer 0 <= X_MONTPELLIER_MARSEILLE <= 1 Integer 0 <= X_MONTPELLIER_MONTPELLIER <= 1 Integer 0 <= X_MONTPELLIER_NANTES <= 1 Integer 0 <= X_MONTPELLIER_NICE <= 1 Integer 0 <= X_MONTPELLIER_RENNES <= 1 Integer 0 <= X_MONTPELLIER_STRASBOURG <= 1 Integer 0 <= X_MONTPELLIER_TOULOUSE <= 1 Integer 0 <= X_NANTES_BORDEAUX <= 1 Integer 0 <= X_NANTES_LILLE <= 1 Integer 0 <= X_NANTES_LYON <= 1 Integer 0 <= X_NANTES_MARSEILLE <= 1 Integer 0 <= X_NANTES_MONTPELLIER <= 1 Integer 0 <= X_NANTES_NANTES <= 1 Integer 0 <= X_NANTES_NICE <= 1 Integer 0 <= X_NANTES_RENNES <= 1 Integer 0 <= X_NANTES_STRASBOURG <= 1 Integer 0 <= X_NANTES_TOULOUSE <= 1 Integer 0 <= X_NICE_BORDEAUX <= 1 Integer 0 <= X_NICE_LILLE <= 1 Integer 0 <= X_NICE_LYON <= 1 Integer 0 <= X_NICE_MARSEILLE <= 1 Integer 0 <= X_NICE_MONTPELLIER <= 1 Integer 0 <= X_NICE_NANTES <= 1 Integer 0 <= X_NICE_NICE <= 1 Integer 0 <= X_NICE_RENNES <= 1 Integer 0 <= X_NICE_STRASBOURG <= 1 Integer 0 <= X_NICE_TOULOUSE <= 1 Integer 0 <= X_RENNES_BORDEAUX <= 1 Integer 0 <= X_RENNES_LILLE <= 1 Integer 0 <= X_RENNES_LYON <= 1 Integer 0 <= X_RENNES_MARSEILLE <= 1 Integer 0 <= X_RENNES_MONTPELLIER <= 1 Integer 0 <= X_RENNES_NANTES <= 1 Integer 0 <= X_RENNES_NICE <= 1 Integer 0 <= X_RENNES_RENNES <= 1 Integer 0 <= X_RENNES_STRASBOURG <= 1 Integer 0 <= X_RENNES_TOULOUSE <= 1 Integer 0 <= X_STRASBOURG_BORDEAUX <= 1 Integer 0 <= X_STRASBOURG_LILLE <= 1 Integer 0 <= X_STRASBOURG_LYON <= 1 Integer 0 <= X_STRASBOURG_MARSEILLE <= 1 Integer 0 <= X_STRASBOURG_MONTPELLIER <= 1 Integer 0 <= X_STRASBOURG_NANTES <= 1 Integer 0 <= X_STRASBOURG_NICE <= 1 Integer 0 <= X_STRASBOURG_RENNES <= 1 Integer 0 <= X_STRASBOURG_STRASBOURG <= 1 Integer 0 <= X_STRASBOURG_TOULOUSE <= 1 Integer 0 <= X_TOULOUSE_BORDEAUX <= 1 Integer 0 <= X_TOULOUSE_LILLE <= 1 Integer 0 <= X_TOULOUSE_LYON <= 1 Integer 0 <= X_TOULOUSE_MARSEILLE <= 1 Integer 0 <= X_TOULOUSE_MONTPELLIER <= 1 Integer 0 <= X_TOULOUSE_NANTES <= 1 Integer 0 <= X_TOULOUSE_NICE <= 1 Integer 0 <= X_TOULOUSE_RENNES <= 1 Integer 0 <= X_TOULOUSE_STRASBOURG <= 1 Integer 0 <= X_TOULOUSE_TOULOUSE <= 1 Integer 0 <= Y_BORDEAUX <= 1 Integer 0 <= Y_LILLE <= 1 Integer 0 <= Y_LYON <= 1 Integer 0 <= Y_MARSEILLE <= 1 Integer 0 <= Y_MONTPELLIER <= 1 Integer 0 <= Y_NANTES <= 1 Integer 0 <= Y_NICE <= 1 Integer 0 <= Y_RENNES <= 1 Integer 0 <= Y_STRASBOURG <= 1 Integer 0 <= Y_TOULOUSE <= 1 Integer
La résolution est alors la suivante :
prob.writeLP("PMed.lp")
prob.solve()
print("Total Cost ", value(prob.objective))
for v in prob.variables():
print(v.name, "=", v.varValue)
Total Cost 2051.226 X_BORDEAUX_BORDEAUX = 0.0 X_BORDEAUX_LILLE = 0.0 X_BORDEAUX_LYON = 0.0 X_BORDEAUX_MARSEILLE = 0.0 X_BORDEAUX_MONTPELLIER = 0.0 X_BORDEAUX_NANTES = 1.0 X_BORDEAUX_NICE = 0.0 X_BORDEAUX_RENNES = 0.0 X_BORDEAUX_STRASBOURG = 0.0 X_BORDEAUX_TOULOUSE = 0.0 X_LILLE_BORDEAUX = 0.0 X_LILLE_LILLE = 0.0 X_LILLE_LYON = 0.0 X_LILLE_MARSEILLE = 0.0 X_LILLE_MONTPELLIER = 0.0 X_LILLE_NANTES = 0.0 X_LILLE_NICE = 0.0 X_LILLE_RENNES = 0.0 X_LILLE_STRASBOURG = 1.0 X_LILLE_TOULOUSE = 0.0 X_LYON_BORDEAUX = 0.0 X_LYON_LILLE = 0.0 X_LYON_LYON = 0.0 X_LYON_MARSEILLE = 0.0 X_LYON_MONTPELLIER = 1.0 X_LYON_NANTES = 0.0 X_LYON_NICE = 0.0 X_LYON_RENNES = 0.0 X_LYON_STRASBOURG = 0.0 X_LYON_TOULOUSE = 0.0 X_MARSEILLE_BORDEAUX = 0.0 X_MARSEILLE_LILLE = 0.0 X_MARSEILLE_LYON = 0.0 X_MARSEILLE_MARSEILLE = 0.0 X_MARSEILLE_MONTPELLIER = 1.0 X_MARSEILLE_NANTES = 0.0 X_MARSEILLE_NICE = 0.0 X_MARSEILLE_RENNES = 0.0 X_MARSEILLE_STRASBOURG = 0.0 X_MARSEILLE_TOULOUSE = 0.0 X_MONTPELLIER_BORDEAUX = 0.0 X_MONTPELLIER_LILLE = 0.0 X_MONTPELLIER_LYON = 0.0 X_MONTPELLIER_MARSEILLE = 0.0 X_MONTPELLIER_MONTPELLIER = 1.0 X_MONTPELLIER_NANTES = 0.0 X_MONTPELLIER_NICE = 0.0 X_MONTPELLIER_RENNES = 0.0 X_MONTPELLIER_STRASBOURG = 0.0 X_MONTPELLIER_TOULOUSE = 0.0 X_NANTES_BORDEAUX = 0.0 X_NANTES_LILLE = 0.0 X_NANTES_LYON = 0.0 X_NANTES_MARSEILLE = 0.0 X_NANTES_MONTPELLIER = 0.0 X_NANTES_NANTES = 1.0 X_NANTES_NICE = 0.0 X_NANTES_RENNES = 0.0 X_NANTES_STRASBOURG = 0.0 X_NANTES_TOULOUSE = 0.0 X_NICE_BORDEAUX = 0.0 X_NICE_LILLE = 0.0 X_NICE_LYON = 0.0 X_NICE_MARSEILLE = 0.0 X_NICE_MONTPELLIER = 1.0 X_NICE_NANTES = 0.0 X_NICE_NICE = 0.0 X_NICE_RENNES = 0.0 X_NICE_STRASBOURG = 0.0 X_NICE_TOULOUSE = 0.0 X_RENNES_BORDEAUX = 0.0 X_RENNES_LILLE = 0.0 X_RENNES_LYON = 0.0 X_RENNES_MARSEILLE = 0.0 X_RENNES_MONTPELLIER = 0.0 X_RENNES_NANTES = 1.0 X_RENNES_NICE = 0.0 X_RENNES_RENNES = 0.0 X_RENNES_STRASBOURG = 0.0 X_RENNES_TOULOUSE = 0.0 X_STRASBOURG_BORDEAUX = 0.0 X_STRASBOURG_LILLE = 0.0 X_STRASBOURG_LYON = 0.0 X_STRASBOURG_MARSEILLE = 0.0 X_STRASBOURG_MONTPELLIER = 0.0 X_STRASBOURG_NANTES = 0.0 X_STRASBOURG_NICE = 0.0 X_STRASBOURG_RENNES = 0.0 X_STRASBOURG_STRASBOURG = 1.0 X_STRASBOURG_TOULOUSE = 0.0 X_TOULOUSE_BORDEAUX = 0.0 X_TOULOUSE_LILLE = 0.0 X_TOULOUSE_LYON = 0.0 X_TOULOUSE_MARSEILLE = 0.0 X_TOULOUSE_MONTPELLIER = 1.0 X_TOULOUSE_NANTES = 0.0 X_TOULOUSE_NICE = 0.0 X_TOULOUSE_RENNES = 0.0 X_TOULOUSE_STRASBOURG = 0.0 X_TOULOUSE_TOULOUSE = 0.0 Y_BORDEAUX = 0.0 Y_LILLE = 0.0 Y_LYON = 0.0 Y_MARSEILLE = 0.0 Y_MONTPELLIER = 1.0 Y_NANTES = 1.0 Y_NICE = 0.0 Y_RENNES = 0.0 Y_STRASBOURG = 1.0 Y_TOULOUSE = 0.0
Si on veut juste connaitre les entrepôts ouverts ou non, on peut juste écrire cela :
v = prob.variables()
l = len(prob.variables())
for i in range(len(y_vars)) :
print(v[l-(i+1)].name, "=", v[l-(i+1)].varValue)
Y_TOULOUSE = 0.0 Y_STRASBOURG = 1.0 Y_RENNES = 0.0 Y_NICE = 0.0 Y_NANTES = 1.0 Y_MONTPELLIER = 1.0 Y_MARSEILLE = 0.0 Y_LYON = 0.0 Y_LILLE = 0.0 Y_BORDEAUX = 0.0
Le problème de couverture maximale¶
Le problème de couverture maximale est un problème d'optimisation combinatoire fondamental qui consiste à sélectionner un nombre minimal de sous-ensembles (l'offre) pour couvrir un maximum d'éléments (la demande), sachant que cette offre doit être située à une distance maximale donnée de la demande. Ce problème est utilisé dans de nombreux domaines et fait l'objet de nombreuses recherches en raison de sa complexité et de son importance pratique. Par exemple, on pourra chercher à placer n installations de telle sorte à couvrir un maximum de personnes dans un rayon donné (x km ou x minutes). C'est sans doute le problème de localisation-allocation le plus utile pour des entreprises commerciales.
Plus concrètement, s'il est important que les citoyens soient situés à moins de 10 minutes d'un service d'urgence et que l'on peut ouvrir 700 services d'urgence en France, le problème de couverture maximale vous donnera les emplacements optimum de ces 700 services d'urgence de telle sorte à couvrir un maximum de personnes dans ce rayon de 10 minutes. Autrement dit, cela minimisera le nombre de personnes situées dans des "zones blanches" (des zones non couvertes, mal desservies par ces services d'urgence...).
Le problème de couverture maximale peut se formaliser de la manière suivante, la fonction objectif cherche à maximiser la demande couverte :
Max $\displaystyle \sum_{i}^{N} D_{i} \times Z_{i} $
Pour cela, il faudra ouvrir un nombre p donné de sites (en tout cas, pas plus que le nombre donné) :
$\displaystyle \sum_{j}^{M} Y_{j} \le p $
Enfin, un site fermé ne peut pas couvrir de clients.
$\displaystyle Z_{i} \le \sum_{j}^{M} A_{i,j} \times Y_{j} $ $ \forall i $
Les variables $Y_{j}$ et $Z_{i}$ sont binaires. $Z_{i}$ = 1 si le lieu de demande i est couvert par au moins un site (rayon maximal respecté), sinon $Z_{i}$ = 0. $Y_{j}$ = 1 si le site est ouvert, sinon $Y_{j}$ = 0. Les valeurs $D_{i}$ correspondent au niveau de demande en un lieu i. Les valeurs $A_{i,j}$ sont égales à 1 si $D_{i,j}$ est inférieure à la distance fixée Dmax, sinon $A_{i,j}$ = 0.
Par exemple, on peut reprendre les données du problème p-median avec les 10 grandes villes françaises du fichier Pmed_Pref.xlsx. On va juste rajouter une liste Demande qui contient les populations (en dizaine de milliers) de ces villes.
import pandas as pd
Dist = pd.read_excel('C:/Users/Serge/Desktop/TP_modlocalloc/Pmed_Pref.xlsx', index_col = 0, header=0)
#Point arrivée
Site = list(Dist.columns)
# Point depart
Usager = list(Dist.index)
#Demande
Demande = [35,23,52,32,22,50,26,87,30,29]
Ensuite, si on cherche à maximiser le nombre de personnes desservies par 3 sites (localisés parmi ces villes) dans un rayon de 250 km, il faut créer un objet permettant de savoir quelles sont les distances inférieures à cette distance maximale.
dmax = 250
a = 1 * (Dist < dmax)
Ce problème est un problème de maximisation et nos variables à résoudre sont les listes des lieux des individus à desservir (z_vars) et la liste des sites potentiels d'implantation (y_vars).
prob = LpProblem("Pset",LpMaximize)
# Declaration variable
y_vars = LpVariable.dicts('Y', Site, lowBound = 0, upBound = 1, cat=LpInteger)
Z_vars = LpVariable.dicts('Z', Usager, lowBound = 0, upBound = 1, cat=LpInteger)
On peut alors écrire les contraintes comme ci-dessous :
# Fonction Objectif
prob += lpSum([Z_vars[i] * Demande[Usager.index(i)] for i in Usager])
# Contrainte 3 Sites
prob += lpSum([y_vars[j] for j in Site]) == 3
# Individus affectes a un site ouvert
for i in Usager :
prob += lpSum([a[j][i] * y_vars[j] for j in Site]) >= Z_vars[i]
Le tour est joué ! On peut couvrir 2,82 millions de personnes (les populations de Bordeaux, Marseille, Montpellier, Nantes, Nice, Rennes et Toulouse) en ouvrant trois sites : Bordeaux, Marseille et Nantes.
# The problem is solved using PuLP's choice of Solver
prob.writeLP("PMax.lp")
prob.solve()
# Affichage Résultat
print("Total Cost ", value(prob.objective))
for v in prob.variables():
print(v.name, "=", v.varValue)
Total Cost 282.0 Y_BORDEAUX = 1.0 Y_LILLE = 0.0 Y_LYON = 0.0 Y_MARSEILLE = 1.0 Y_MONTPELLIER = 0.0 Y_NANTES = 1.0 Y_NICE = 0.0 Y_RENNES = 0.0 Y_STRASBOURG = 0.0 Y_TOULOUSE = 0.0 Z_BORDEAUX = 1.0 Z_LILLE = 0.0 Z_LYON = 0.0 Z_MARSEILLE = 1.0 Z_MONTPELLIER = 1.0 Z_NANTES = 1.0 Z_NICE = 1.0 Z_RENNES = 1.0 Z_STRASBOURG = 0.0 Z_TOULOUSE = 1.0